Для начала — немного лирики, чтобы почувствовать проблему, которую решает метод интервалов. Допустим, нам надо решить вот такое неравенство:
(x − 5)(x + 3) > 0
Какие есть варианты? Первое, что приходит в голову большинству учеников — это правила «плюс на плюс дает плюс» и «минус на минус дает плюс». Поэтому достаточно рассмотреть случай, когда обе скобки положительны: x − 5 > 0 и x + 3 > 0. Затем также рассмотрим случай, когда обе скобки отрицательны: x − 5 < 0 и x + 3 < 0. Таким образом, наше неравенство свелось к совокупности двух систем, которая, впрочем, легко решается:
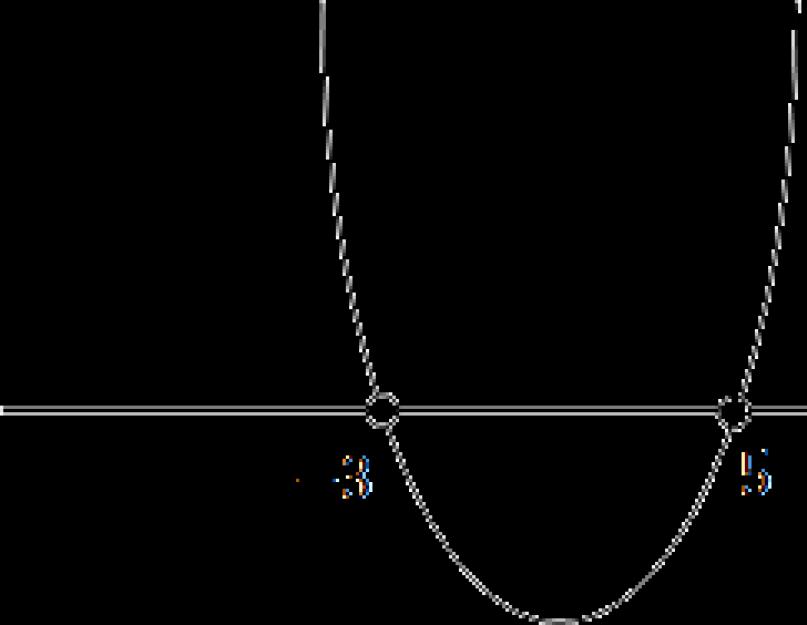
Более продвинутые ученики вспомнят (может быть), что слева стоит квадратичная функция, график которой — парабола. Причем эта парабола пересекает ось OX в точках x = 5 и x = −3. Для дальнейшей работы надо раскрыть скобки. Имеем:
x 2 − 2x − 15 > 0
Теперь понятно, что ветви параболы направлены вверх, т.к. коэффициент a = 1 > 0. Попробуем нарисовать схему этой параболы:

Функция больше нуля там, где она проходит выше оси OX . В нашем случае это интервалы (−∞ −3) и (5; +∞) — это и есть ответ.
Обратите внимание: на рисунке изображена именно схема функции , а не ее график. Потому что для настоящего графика надо считать координаты, рассчитывать смещения и прочую хрень, которая нам сейчас совершенно ни к чему.
Почему эти методы неэффективны?
Итак, мы рассмотрели два решения одного и того же неравенства. Оба они оказались весьма громоздкими. В первом решении возникает — вы только вдумайтесь! — совокупность систем неравенств. Второе решение тоже не особо легкое: нужно помнить график параболы и еще кучу мелких фактов.
Это было очень простое неравенство. В нем всего 2 множителя. А теперь представьте, что множителей будет не 2, а хотя бы 4. Например:
(x − 7)(x − 1)(x + 4)(x + 9) < 0
Как решать такое неравенство? Перебирать все возможные комбинации плюсов и минусов? Да мы уснем быстрее, чем найдем решение. Рисовать график — тоже не вариант, поскольку непонятно, как ведет себя такая функция на координатной плоскости.
Для таких неравенств нужен специальный алгоритм решения, который мы сегодня и рассмотрим.
Что такое метод интервалов
Метод интервалов — это специальный алгоритм, предназначенный для решения сложных неравенств вида f (x ) > 0 и f (x ) < 0. Алгоритм состоит из 4 шагов:
- Решить уравнение f (x ) = 0. Таким образом, вместо неравенства получаем уравнение, которое решается намного проще;
- Отметить все полученные корни на координатной прямой. Таким образом, прямая разделится на несколько интервалов;
- Выяснить знак (плюс или минус) функции f (x ) на самом правом интервале. Для этого достаточно подставить в f (x ) любое число, которое будет правее всех отмеченных корней;
- Отметить знаки на остальных интервалах. Для этого достаточно запомнить, что при переходе через каждый корень знак меняется.
Вот и все! После этого останется лишь выписать интервалы, которые нас интересуют. Они отмечены знаком «+», если неравенство имело вид f (x ) > 0, или знаком «−», если неравенство имеет вид f (x ) < 0.
На первый взгляд может показаться, что метод интервалов — это какая-то жесть. Но на практике все будет очень просто. Стоит чуть-чуть потренироваться — и все станет понятно. Взгляните на примеры — и убедитесь в этом сами:
Задача. Решите неравенство:
(x − 2)(x + 7) < 0
Работаем по методу интервалов. Шаг 1: заменяем неравенство уравнением и решаем его:
(x − 2)(x + 7) = 0
Произведение равно нулю тогда и только тогда, когда хотя бы один из множителей равен нулю:
x
− 2 = 0 ⇒ x
= 2;
x
+ 7 = 0 ⇒ x
= −7.
Получили два корня. Переходим к шагу 2: отмечаем эти корни на координатной прямой. Имеем:
Теперь шаг 3: находим знак функции на самом правом интервале (правее отмеченной точки x = 2). Для этого надо взять любое число, которое больше числа x = 2. Например, возьмем x = 3 (но никто не запрещает взять x = 4, x = 10 и даже x = 10 000). Получим:
f
(x
) = (x
− 2)(x
+ 7);
x
= 3;
f
(3) = (3 − 2)(3 + 7) = 1 · 10 = 10;
Получаем, что f (3) = 10 > 0, поэтому в самом правом интервале ставим знак плюс.
Переходим к последнему пункту — надо отметить знаки на остальных интервалах. Помним, что при переходе через каждый корень знак должен меняться. Например, справа от корня x = 2 стоит плюс (мы убедились в этом на предыдущем шаге), поэтому слева обязан стоять минус.
Этот минус распространяется на весь интервал (−7; 2), поэтому справа от корня x = −7 стоит минус. Следовательно, слева от корня x = −7 стоит плюс. Осталось отметить эти знаки на координатной оси. Имеем:
Вернемся к исходному неравенству, которое имело вид:
(x − 2)(x + 7) < 0
Итак, функция должна быть меньше нуля. Значит, нас интересует знак минус, который возникает лишь на одном интервале: (−7; 2). Это и будет ответ.
Задача. Решите неравенство:
(x + 9)(x − 3)(1 − x ) < 0
Шаг 1: приравниваем левую часть к нулю:
(x
+ 9)(x
− 3)(1 − x
) = 0;
x
+ 9 = 0 ⇒ x
= −9;
x
− 3 = 0 ⇒ x
= 3;
1 − x
= 0 ⇒ x
= 1.
Помните: произведение равно нулю, когда хотя бы один из множителей равен нулю. Именно поэтому мы вправе приравнять к нулю каждую отдельную скобку.
Шаг 2: отмечаем все корни на координатной прямой:
Шаг 3: выясняем знак самого правого промежутка. Берем любое число, которое больше, чем x = 1. Например, можно взять x = 10. Имеем:
f
(x
) = (x
+ 9)(x
− 3)(1 − x
);
x
= 10;
f
(10) = (10 + 9)(10 − 3)(1 − 10) = 19 · 7 · (−9) = − 1197;
f
(10) = −1197 < 0.
Шаг 4: расставляем остальные знаки. Помним, что при переходе через каждый корень знак меняется. В итоге наша картинка будет выглядеть следующим образом:
Вот и все. Осталось лишь выписать ответ. Взгляните еще раз на исходное неравенство:
(x + 9)(x − 3)(1 − x ) < 0
Это неравенство вида f (x ) < 0, т.е. нас интересуют интервалы, отмеченные знаком минус. А именно:
x ∈ (−9; 1) ∪ (3; +∞)
Это и есть ответ.
Замечание по поводу знаков функции
Практика показывает, что наибольшие трудности в методе интервалов возникают на последних двух шагах, т.е. при расстановке знаков. Многие ученики начинают путаться: какие надо брать числа и где ставить знаки.
Чтобы окончательно разобраться в методе интервалов, рассмотрим два замечания, на которых он построен:
- Непрерывная функция меняет знак только в тех точках, где она равна нулю . Такие точки разбивают координатную ось на куски, внутри которых знак функции никогда не меняется. Вот зачем мы решаем уравнение f (x ) = 0 и отмечаем найденные корни на прямой. Найденные числа — это «пограничные» точки, отделяющие плюсы от минусов.
- Чтобы выяснить знак функции на каком-либо интервале, достаточно подставить в функцию любое число из этого интервала. Например, для интервала (−5; 6) мы вправе брать x = −4, x = 0, x = 4 и даже x = 1,29374, если нам захочется. Почему это важно? Да потому что многих учеников начинают грызть сомнения. Мол, что если для x = −4 мы получим плюс, а для x = 0 — минус? А ничего — такого никогда не будет. Все точки на одном интервале дают один и тот же знак. Помните об этом.
Вот и все, что нужно знать про метод интервалов. Конечно, мы разобрали его в самом простом варианте. Существуют более сложные неравенства — нестрогие, дробные и с повторяющимися корнями. Для них тоже можно применять метод интервалов, но это тема для отдельного большого урока.
Теперь хотел бы разобрать продвинутый прием, который резко упрощает метод интервалов. Точнее, упрощение затрагивает только третий шаг — вычисление знака на самом правом куске прямой. По каким-то причинам этот прием не проходят в школах (по крайней мере, мне никто такого не объяснял). А зря — ведь на самом деле этот алгоритм очень прост.
Итак, знак функции на правом куске числовой оси. Этот кусок имеет вид (a ; +∞), где a — самый большой корень уравнения f (x ) = 0. Чтобы не взрывать мозг, рассмотрим конкретный пример:
(x
− 1)(2 + x
)(7 − x
) < 0;
f
(x
) = (x
− 1)(2 + x
)(7 − x
);
(x
− 1)(2 + x
)(7 − x
) = 0;
x
− 1 = 0 ⇒ x
= 1;
2 + x
= 0 ⇒ x
= −2;
7 − x
= 0 ⇒ x
= 7;
Мы получили 3 корня. Перечислим их в порядке возрастания: x = −2, x = 1 и x = 7. Очевидно, что наибольший корень — это x = 7.
Для тех, кому легче рассуждать графически, я отмечу эти корни на координатной прямой. Посмотрим, что получится:
Требуется найти знак функции f (x ) на самом правом интервале, т.е. на (7; +∞). Но как мы уже отмечали, для определения знака можно взять любое число из этого интервала. Например, можно взять x = 8, x = 150 и т.д. А теперь — тот самый прием, который не проходят в школах: давайте в качестве числа возьмем бесконечность. Точнее, плюс бесконечность , т.е. +∞.
«Ты че, обкурился? Как можно подставить в функцию бесконечность?» — возможно, спросите вы. Но задумайтесь: нам ведь не нужно само значение функции, нам нужен только знак. Поэтому, например, значения f (x ) = −1 и f (x ) = −938 740 576 215 значат одно и то же: функция на данном интервале отрицательна. Поэтому все, что от вас требуется — найти знак, который возникает на бесконечности, а не значение функции.
На самом деле, подставлять бесконечность очень просто. Вернемся к нашей функции:
f (x ) = (x − 1)(2 + x )(7 − x )
Представьте, что x — это очень большое число. Миллиард или даже триллион. Теперь посмотрим, что будет происходить в каждой скобке.
Первая скобка: (x − 1). Что будет, если из миллиарда вычесть единицу? Получится число, не особо отличающееся от миллиарда, и это число будет положительным. Аналогично со второй скобкой: (2 + x ). Если к двойке прибавить миллиард, по получим миллиард с копейками — это положительное число. Наконец, третья скобка: (7 − x ). Здесь будет минус миллиард, от которого «отгрызли» жалкий кусочек в виде семерки. Т.е. полученное число мало чем будет отличаться от минус миллиарда — оно будет отрицательным.
Осталось найти знак всего произведения. Поскольку в первых скобках у нас был плюс, а в последней — минус, получаем следующую конструкцию:
(+) · (+) · (−) = (−)
Итоговый знак — минус! И неважно, чему равно значение самой функции. Главное, что это значение — отрицательное, т.е. на самом правом интервале стоит знак минус. Осталось выполнить четвертый шаг метода интервалов: расставить все знаки. Имеем:
Исходное неравенство имело вид:
(x − 1)(2 + x )(7 − x ) < 0
Следовательно, нас интересуют интервалы, отмеченные знаком минус. Выписываем ответ:
x ∈ (−2; 1) ∪ (7; +∞)
Вот и весь прием, который я хотел рассказать. В заключение — еще одно неравенство, которое решается методом интервалов с привлечением бесконечности. Чтобы визуально сократить решение, я не буду писать номера шагов и развернутые комментарии. Напишу только то, что действительно надо писать при решении реальных задач:
Задача. Решите неравенство:
x (2x + 8)(x − 3) > 0
Заменяем неравенство уравнением и решаем его:
x
(2x
+ 8)(x
− 3) = 0;
x
= 0;
2x
+ 8 = 0 ⇒ x
= −4;
x
− 3 = 0 ⇒ x
= 3.
Отмечаем все три корня на координатной прямой (сразу со знаками):
Справа на координатной оси стоит плюс, т.к. функция имеет вид:
f (x ) = x (2x + 8)(x − 3)
А если подставить бесконечность (например, миллиард), получим три положительных скобки. Поскольку исходное выражение должно быть больше нуля, нас интересуют только плюсы. Осталось выписать ответ:
x ∈ (−4; 0) ∪ (3; +∞)
Что нужно знать о значках неравенств? Неравенства со значком больше (> ), или меньше (< ) называются строгими. Со значками больше или равно (≥ ), меньше или равно (≤ ) называются нестрогими. Значок не равно (≠ ) стоит особняком, но решать примеры с таким значком тоже приходится постоянно. И мы порешаем.)
Сам значок не оказывает особого влияния на процесс решения. А вот в конце решения, при выборе окончательного ответа, смысл значка проявляется в полную силу! Что мы и увидим ниже, на примерах. Есть там свои приколы...
Неравенства, как и равенства, бывают верные и неверные. Здесь всё просто, без фокусов. Скажем, 5 > 2 - верное неравенство. 5 < 2 - неверное.
Такая подготовка работает для неравенств любого вида и проста до ужаса.) Нужно, всего лишь, правильно выполнять два (всего два!) элементарных действия. Эти действия знакомы всем. Но, что характерно, косяки в этих действиях - и есть основная ошибка в решении неравенств, да... Стало быть, надо повторить эти действия. Называются эти действия вот как:
Тождественные преобразования неравенств.
Тождественные преобразования неравенств очень похожи на тождественные преобразования уравнений. Собственно, в этом и есть основная проблема. Отличия проскакивают мимо головы и... приехали.) Поэтому я особо выделю эти отличия. Итак, первое тождественное преобразование неравенств:
1. К обеим частям неравенства можно прибавить (отнять) одно и то же число, или выражение. Любое. Знак неравенства от этого не изменится.
На практике это правило применяется как перенос членов из левой части неравенства в правую (и наоборот) со сменой знака. Со сменой знака члена, а не неравенства! Правило один в один совпадает с правилом для уравнений. А вот следующие тождественные преобразования в неравенствах существенно отличается от таковых в уравнениях. Поэтому я выделяю их красным цветом:
2. Обе части неравенства можно умножить (разделить) на одно и то же положительное число. На любое положительное не изменится.
3. Обе части неравенства можно умножить (разделить) на одно и то же отрицательное число. На любое отрицательное число. Знак неравенства от этого изменится на противоположный.
Вы помните (надеюсь...), что уравнение можно умножать/делить на что попало. И на любое число, и на выражение с иксом. Лишь бы не на ноль. Ему, уравнению, от этого ни жарко, ни холодно.) Не меняется оно. А вот неравенства более чувствительны к умножению/делению.
Наглядный пример на долгую память. Напишем неравенство, не вызывающее сомнений:
5 > 2
Умножим обе части на +3, получим:
15 > 6
Возражения есть? Возражений нет.) А если умножим обе части исходного неравенства на -3, получим:
15 > -6
А это уже откровенная ложь.) Полное враньё! Обман народа! Но стоит изменить знак неравенства на противоположный, как всё становится на свои места:
15 < -6
Про враньё и обман - это я не просто так ругаюсь.) "Забыл сменить знак неравенства..." - это главная ошибка в решении неравенств. Это пустяковое и несложное правило стольких людей ушибло! Которые забыли...) Вот и ругаюсь. Может, запомнится...)
Особо внимательные заметят, что неравенство нельзя умножать на выражение с иксом. Респект внимательным!) А почему нельзя? Ответ простой. Мы же не знаем знак этого выражения с иксом. Оно может быть положительное, отрицательное... Стало быть, мы не знаем, какой знак неравенства ставить после умножения. Менять его, или нет? Неизвестно. Разумеется, это ограничение (запрет умножения/деления неравенства на выражение с иксом) можно обойти. Если очень надо будет. Но это тема для других уроков.
Вот и все тождественные преобразования неравенств. Ещё раз напомню, что они работают для любых неравенств. А теперь можно переходить к конкретным видам.
Линейные неравенства. Решение, примеры.
Линейными неравенствами называются неравенства, в которых икс находится в первой степени и нет деления на икс. Типа:
х+3 > 5х-5
Как решаются такие неравенства? Они решаются очень просто! А именно: с помощью сводим самое замороченное линейное неравенство прямо к ответу. Вот и всё решение. Главные моменты решения я буду выделять. Во избежание дурацких ошибок.)
Решаем это неравенство:
х+3 > 5х-5
Решаем точно так же, как и линейное уравнение. С единственным отличием:
Внимательно следим за знаком неравенства!
Первый шаг самый обычный. С иксами - влево, без иксов - вправо... Это первое тождественное преобразование, простое и безотказное.) Только знаки у переносимых членов не забываем менять.
Знак неравенства сохраняется:
х-5х > -5-3
Приводим подобные.
Знак неравенства сохраняется:
4х > -8
Осталось применить последнее тождественное преобразование: разделить обе части на -4.
Делим на отрицательное число.
Знак неравенства изменится на противоположный:
х < 2
Это ответ.
Так решаются все линейные неравенства.
Внимание! Точка 2 рисуется белой, т.е. незакрашенной. Пустой внутри. Это означает, что она в ответ не входит! Я её специально такой здоровой нарисовал. Такая точка (пустая, а не здоровая!)) в математике называется выколотой точкой.
Остальные числа на оси отмечать можно, но не нужно. Посторонние числа, не относящиеся к нашему неравенству, могут и запутать, да... Нужно только помнить, что увеличение чисел идёт по стрелке, т.е. числа 3, 4, 5, и т.д. находятся правее двойки, а числа 1, 0, -1 и т.д. - левее.
Неравенство х < 2 - строгое. Икс строго меньше двух. Если возникают сомнения, проверка простая. Подставляем сомнительное число в неравенство и размышляем: "Два меньше двух? Нет, конечно!" Именно так. Неравенство 2 < 2 неверное. Не годится двойка в ответ.
А единичка годится? Конечно. Меньше же... И ноль годится, и -17, и 0,34... Да все числа, которые меньше двух - годятся! И даже 1,9999.... Хоть чуть чуть, да меньше!
Вот и отметим все эти числа на числовой оси. Как? Тут бывают варианты. Вариант первый - штриховка. Наводим мышку на рисунок (или касаемся картинки на планшете) и видим, что заштрихована область всех иксов, подходящих под условие х < 2 . Вот и всё.
Второй вариант рассмотрим на втором примере:
х ≥ -0,5
Рисуем ось, отмечаем число -0,5. Вот так:
Заметили разницу?) Ну да, трудно не заметить... Эта точка - чёрная! Закрашенная. Это означает, что -0,5 входит в ответ. Здесь, кстати, проверка и смутить может кого-нибудь. Подставляем:
-0,5 ≥ -0,5
Как так? -0,5 никак не больше -0,5! А значок больше имеется...
Ничего страшного. В нестрогом неравенстве годится всё, что подходит под значок. И равно годится, и больше годится. Следовательно, -0,5 в ответ включается.
Итак, -0,5 мы отметили на оси, осталось ещё отметить все числа, которые больше -0,5. На этот раз я отмечаю область подходящих значений икса дужкой (от слова дуга ), а не штриховкой. Наводим курсор на рисунок и видим эту дужку.
Особой разницы между штриховкой и дужками нет. Делайте, как учитель сказал. Если учителя нет - рисуйте дужки. В более сложных заданиях штриховка менее наглядна. Запутаться можно.
Вот так рисуются линейные неравенства на оси. Переходим к следующей особенности неравенств.
Запись ответа для неравенств.
В уравнениях было хорошо.) Нашли икс, да и записали ответ, например: х=3. В неравенствах существуют две формы записи ответов. Одна - в виде окончательного неравенства. Хороша для простых случаев. Например:
х < 2.
Это полноценный ответ.
Иногда требуется записать то же самое, но в другой форме, через числовые промежутки. Тогда запись начинает выглядеть очень научно):
х ∈ (-∞; 2)
Под значком ∈ скрывается слово "принадлежит".
Читается запись так: икс принадлежит промежутку от минус бесконечности до двух не включая . Вполне логично. Икс может быть любым числом из всех возможных чисел от минус бесконечности до двух. Двойкой икс быть не может, о чём нам и говорит слово "не включая".
А где это в ответе видно, что "не включая" ? Этот факт отмечается в ответе круглой скобкой сразу после двойки. Если бы двойка включалась, скобка была бы квадратной. Вот такой: ]. В следующем примере такая скобка используется.
Запишем ответ: х ≥ -0,5 через промежутки:
х ∈ [-0,5; +∞)
Читается: икс принадлежит промежутку от минус 0,5, включая, до плюс бесконечности.
Бесконечность не может включаться никогда. Это не число, это символ. Поэтому в подобных записях бесконечность всегда соседствует с круглой скобкой.
Такая форма записи удобна для сложных ответов, состоящих из нескольких промежутков. Но - именно для окончательных ответов. В промежуточных результатах, где предполагается дальнейшее решение, лучше использовать обычную форму, в виде простого неравенства. Мы с этим в соответствующих темах разберёмся.
Популярные задания с неравенствами.
Сами по себе линейные неравенства просты. Поэтому, частенько, задания усложняются. Так, чтобы подумать надо было. Это, если с непривычки, не очень приятно.) Но полезно. Покажу примеры таких заданий. Не для того, чтобы вы их выучили, это лишнее. А для того, чтобы не боялись при встрече с подобными примерами. Чуть подумать - и всё просто!)
1. Найдите любые два решения неравенства 3х - 3 < 0
Если не очень понятно, что делать, вспоминаем главное правило математики:
Не знаешь, что нужно - делай, что можно!)
х < 1
И что? Да ничего особенного. Что нас просят? Нас просят найти два конкретных числа, которые являются решением неравенства. Т.е. подходят под ответ. Два любых числа. Собственно, это и смущает.) Подходит парочка 0 и 0,5. Парочка -3 и -8. Да этих парочек бесконечное множество! Какой ответ правильный?!
Отвечаю: все! Любая парочка чисел, каждое из которых меньше единицы, будет правильным ответом. Пишите, какую хотите. Едем дальше.
2. Решить неравенство:
4х - 3 ≠ 0
Задания в таком виде встречаются редко. Но, как вспомогательные неравенства, при нахождении ОДЗ, например, или при нахождении области определения функции, - встречаются сплошь и рядом. Такое линейное неравенство можно решать как обычное линейное уравнение. Только везде, кроме знака "=" (равно ) ставить знак "≠ " (не равно ). Так к ответу и подойдёте, со знаком неравенства:
х ≠ 0,75
В более сложных примерах, лучше поступать по-другому. Сделать из неравенства равенство. Вот так:
4х - 3 = 0
Спокойно решить его, как учили, и получить ответ:
х = 0,75
Главное, в самом конце, при записи окончательного ответа, не забыть, что мы нашли икс, который даёт равенство. А нам нужно - неравенство. Стало быть, этот икс нам как раз и не нужен.) И надо записать его с правильным значком:
х ≠ 0,75
При таком подходе получается меньше ошибок. У тех, кто уравнения на автомате решает. А тем, кто уравнения не решает, неравенства, собственно, ни к чему...) Ещё пример популярного задания:
3. Найти наименьшее целое решение неравенства:
3(х - 1) < 5х + 9
Сначала просто решаем неравенство. Ракрываем скобки, переносим, приводим подобные... Получаем:
х > - 6
Не так получилось!? А за знаками следили!? И за знаками членов, и за знаком неравенства...
Опять соображаем. Нам нужно найти конкретное число, подходящее и под ответ, и под условие "наименьшее целое". Если сразу не осеняет, можно просто взять любое число и прикинуть. Два больше минус шести? Конечно! А есть подходящее число поменьше? Разумеется. Например, ноль больше -6. А ещё меньше? Нам же самое маленькое из возможных надо! Минус три больше минус шести! Уже можно уловить закономерность и перестать тупо перебирать числа, правда?)
Берём число поближе к -6. Например, -5. Ответ выполняется, -5 > - 6. Можно найти ещё число, меньше -5, но больше -6? Можно, например -5,5... Стоп! Нам сказано целое решение! Не катит -5,5! А минус шесть? Э-э-э! Неравенство строгое, минус 6 никак не меньше минус 6!
Стало быть, правильный ответ: -5.
Надеюсь, с выбором значения из общего решения всё понятно. Ещё пример:
4. Решить неравенство:
7 < 3х+1 < 13
Во как! Такое выражение называется тройным неравенством. Строго говоря, это сокращённая запись системы неравенств. Но решать такие тройные неравенства всё равно приходится в некоторых заданиях... Оно решается безо всяких систем. По тем же тождественным преобразованиям.
Надо упростить, довести это неравенство до чистого икса. Но... Что куда переносить!? Вот тут самое время вспомнить, что перенос влево-вправо, это сокращённая форма первого тождественного преобразования.
А полная форма звучит вот как: К обеим частям уравнения (неравенства) можно прибавить/отнять любое число, или выражение.
Здесь три части. Вот и будем применять тождественные преобразования ко всем трём частям!
Итак, избавимся от единички в средней части неравенства. Отнимем от всей средней части единичку. Чтобы неравенство не изменилось, отнимем единичку и от оставшихся двух частей. Вот так:
7 -1< 3х+1-1< 13-1
6 < 3х < 12
Уже лучше, правда?) Осталось разделить все три части на тройку:
2 < х < 4
Вот и всё. Это ответ. Икс может любым числом от двойки (не включая) до четвёрки (не включая). Этот ответ тоже записывается через промежутки, такие записи будут в квадратных неравенствах. Там они - самое обычное дело.
В конце урока повторю самое главное. Успех в решении линейных неравенств зависит от умения преобразовывать и упрощать линейные уравнения. Если при этом следить за знаком неравенства, проблем не будет. Чего я вам и желаю. Отсутствия проблем.)
Если Вам нравится этот сайт...
Кстати, у меня есть ещё парочка интересных сайтов для Вас.)
Можно потренироваться в решении примеров и узнать свой уровень. Тестирование с мгновенной проверкой. Учимся - с интересом!)
можно познакомиться с функциями и производными.
Внимание!
К этой теме имеются дополнительные
материалы в Особом разделе 555.
Для тех, кто сильно "не очень..."
И для тех, кто "очень даже...")
Что такое "квадратное неравенство"? Не вопрос!) Если взять любое квадратное уравнение и заменить в нём знак "=" (равно) на любой значок неравенства (> ≥ < ≤ ≠ ), получится квадратное неравенство. Например:
1. x 2 -8x+12 ≥ 0
2. -x 2 +3x > 0
3. x 2 ≤ 4
Ну, вы поняли...)
Я не зря здесь связал уравнения и неравенства. Дело в том, что первый шаг в решении любого квадратного неравенства - решить уравнение, из которого это неравенство сделано. По этой причине - неспособность решать квадратные уравнения автоматически приводит к полному провалу и в неравенствах. Намёк понятен?) Если что, посмотрите, как решать любые квадратные уравнения. Там всё подробно расписано. А в этом уроке мы займёмся именно неравенствами.
Готовое для решения неравенство имеет вид: слева - квадратный трёхчлен ax 2 +bx+c , справа - ноль. Знак неравенства может быть абсолютно любой. Первые два примера здесь уже готовы к решению. Третий пример надо ещё подготовить.
Если Вам нравится этот сайт...
Кстати, у меня есть ещё парочка интересных сайтов для Вас.)
Можно потренироваться в решении примеров и узнать свой уровень. Тестирование с мгновенной проверкой. Учимся - с интересом!)
можно познакомиться с функциями и производными.